In a recent Google+ post, I shared an animation that sliced a tetrahedron along the six planes of symmetry and casually mentioned that the 24 colored regions corresponded to the permutations of $\{1,2,3,4\}$.
Here is a new animation that highlights the appearance of permutations of $\{1,2,3,4\}$.
We label the four vertices of the tetrahedron by the numbers $1$, $2$, $3$, and $4$. When we do this, we see that any automorphism of the tetrahedron reorders the labels of the vertices, which is simply a permutation of $\{1,2,3,4\}$. (I use the technical term "automorphism" to mean any way to rotate or reflect then rotate the tetrahedron and get back the same shape afterward.)
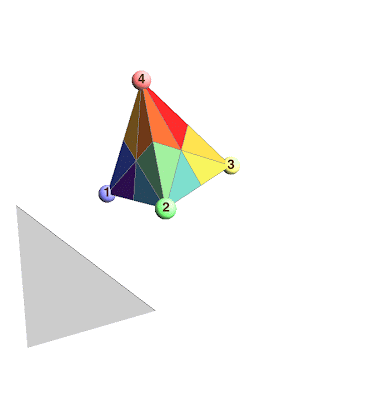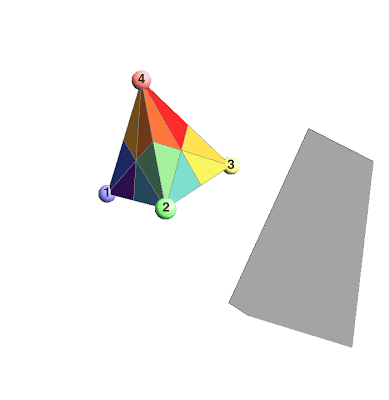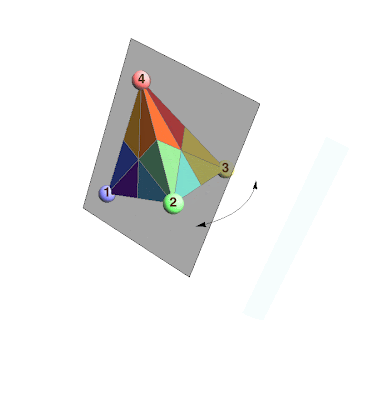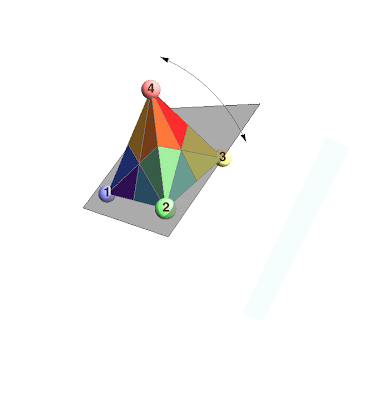
In the animation above, I highlight three special reflections:
$R_1$: The transposition of vertices 1 and 2
$R_2$: The transposition of vertices 2 and 3
$R_3$: The transposition of vertices 3 and 4
They are special because every permutation of $\{1,2,3,4\}$ can be generated by a sequence of these reflections. For example, if we apply the reflection $R_1$ first, then $R_2$ second, and then $R_3$ third, this corresponds to starting with $1234$, switching the first two positions to get $2134$, then switching the two middle positions to get $2314$, and finally switching the last two positions to get $2341$. So we might write that the product $R_1\cdot R_2\cdot R_3$ equals the permutation $2341$.
Of course this equality depends on your convention for the order in which you multiply elements, left to right or right to left, and that is a post for another time.